格拉斯曼: 扩展的学问与线之代数丨贤说八道

我的大学是布满迷惑而百思不得其解的时光。理工科大学生也许都学过一门课，叫线性代数，英文是linear algebra，笔者也未能免俗。印象中我学过的线性代数里，有如下说法：关于n个基 e₁, e₂,…,e_n ，若是关系 α₁e₁+α₂e₂+…+α_ne_n=0 要求 α₁, α₂,…,α_n 全为0，则称它们是线性自力的。至于为啥要提线性自力这个茬儿，为什么充要前提是如许的，那就天知道了 (如今我知道是触碰空间维度的天花板了) 。然后又学了矩阵，关于矩阵有determinant，汉译矩阵值 (多项式方程也有determinant 啊？你分明看见了动词determine，它应该决意个什么呢)。若何求矩阵值呢？书里给个 3×3 矩阵的例子，有六项，三正三负。那么哪个正哪个负呢？书里在矩阵上画了线条，说是为了匡助记忆 (印象中绘图匡助记忆的，还有热力学里的麦克斯韦关系。不讲清楚学问而花功夫教别人记忆，都属于耍混混) 。此外，求矩阵Q的本征值，是解代数方程  ，对应分歧本征值的本征矢量都是线性自力的。要害是，为什么这么求，这些方式都是哪儿来的，又有些什么寄义？我是一概不知。

然后就是学了点经典力学、电动力学，那边面有叉乘的概念，好比角动量界说为 L=r×p，磁场下的洛伦兹力为 F=qv×B，但这里r,p,v分明是矢量，而磁场 B 据说是轴矢量或曰赝矢量，那么这两处的叉乘应该不是一回事儿吗吧？叉乘和求矩阵值的算法有关联吗？不知道，我也没想过。

先说用代数证实几许题。1679年，莱布尼兹畅想应有一种普适代数 (universal algebra)，能斩钉截铁地 (directly and simply) 处理几许对象。这一点在欧几里得的几许里其实已实践过，只是我才刚学到，有点大惊小怪。考查三角形ABC底边BC边上的一点D，则三角形ABD与三角形ABC面积之比为BD/BC。这个问题的证实能够直接写成  ，意思是等式左边的分子、分母从左侧乘以A即可。三角形ABC 就是A和BC乘积的究竟。至于这个“乘法”是什么意思，不焦急，这就是我们要组织和诠释的学问啊！你记住，乘积只是更高阶幂的组织 (construction of a high power)，这句话对懂得代数学有效。注重，对于D为BC地点的直线上的随意一点，等式  都成立 (图1)。此外，若是介意点D是在线段BC的哪一侧，还能够付与线段以偏向。 的取值可正可负，则 也应可正可负，这解说三角形是个有两种取向 (oriented) 或者的几许对象。这一点很轻易懂得。对于平面上随意一个简洁的闭合路径，老是有两个绕行的偏向——会走路的人都知道。这里需要指明的是，单个字母A代表一个点，两个字母相乘获得的AB代表一个线段，而三个字母相乘ABC代表一个三角形。至于乘是什么意思，再说，我们能够成长如许的学问啊。如许的关于几许的代数，正如莱布尼兹所等候的那样，斩钉截铁。这里，从点到线段到面，是靠一个乘法扩睁开来的，这里隐藏着扩展的学问。新鲜吧？

欧几里得的几许有两个元素，点和线 (段)。那么三角形是啥？三角形由三个线段组成的闭合线所围成的一块面积，它能够看作是由两个共点的 (有取向的) 线段所决意的 (有取向的线段现在称为simplices)。是以，这个三角形，有取向的，是由两条有取向的线段经由某种积所决意的。三角形是linear product (线之积)的究竟。AB=A'B' ，两线段长度相等，取向沟通；ABC=A'B'C' ，三角形外形全同，取向沟通。

图1. 共享一个极点且底边共线的多数三角形

考查一条线段ABC，B在中央时，人人轻易接管 AB+BC=AC 。可是，若是给线段以偏向，则有 AB=-BA，那么不管一条线上A、B、C三点是若何放置的，总有 AB+BC=AC 。能够移项，得 AB=AC-BC=AC+CB。对于AB=-BA ，把AB看作是A、B之间的一种乘积，具有性质 AB=-BA 的乘积就组成了一种新的代数，外代数 (exterior algebra) 。

用A, B…如许的单个字母代表点，AB是A, B的积，有性质 AB=-BA 。由此得 ，A²=0，A就是格拉斯曼数。引入实数 α+β=1 ，记P=αA+βB，则 AP=βAB，PB=αAB ，故有 AB=AP+PB，P是AB上的一个点 (这里是数与点的乘积)。注重，两个点之差是矢量 (the difference of two points is a vector)，则 (A-B)+B=A 意思是矢量 (A-B) 以“+”这种把持把点B酿成了A (你把这个把持注释成搬动，那就是诠释了)。

有了这套学问，几许就好办了。设A, B, C 是三角形三极点，设D是AB边上的一点， E是AC边上的一点，且离别将双方长分成沟通的比例。则有，D=(1-α)A+αB ，E=(1-α)A+αC ，两式相减，得 D-E=α(B-C) 。啥意思？就是 D-E与 (B-C) 平行，长度比为 α 。D-E=α(B-C) 透露两线段平行，何等尽收眼底啊。再举一例。证实平行四边形的对角线等分之。对平行四边形ABCD，有A-B=D-C， 移项得 A=D-C+B 。从右侧接连乘上B, C，得 ABC=DBC。换一种移项体式，得 A-B+C=D ，从左侧接连乘上B，A，得 ABC=ABD 。如许 ABD=DBC。QED。整个证实过程就是用到代数的加减和乘法。有了如许的代数几许，几许就是一道代数题  (别跟代数几许弄混了。谁人学问太难！)

有些的读者或者注重到了，把乘法形式的 AB 和减法形式的 A-B 都看成矢量没有矛盾，它们都知足反交流的性质。还记得整数依据惯常的加法组成加法群吗？谁人加法对于整数就有群论意义下的乘法的功能。这只是记号问题。

再看若何解线性方程组。1853年，法国数学家柯西揭橥了一篇论代数钥匙的论文 (Augustin Cauchy, sur les clefs algébriques, Comptes Rendus, 1853)。为简洁起见，以二元线性方程组为例，求解

为此，引入一对柯西所谓的钥匙 (key, clef) i, j, 它们有性质 ii=0；jj=0；ij=-ji  (这恰是外代数的性质)。对方程各自乘上一个钥匙，变为

两式相加，得 (a₁i+a₂j)x+(b₁i+b₂j)y=(c₁i+c₂j)。

神奇时刻来了。注重，对于ii=0；jj=0；ij=-ji  ，任何组合 αi+βj 也有性质 (αi+βj)(αi+βj)=0 。所以，对方程 (a₁i+a₂j)x+(b₁i+b₂j)y=(c₁i+c₂j) 双方离别乘上x和y的系数，使得该项的系数为零 (好神奇的消元法)，直接得

学过固体物理的研究生，从这个解的表达式里就能看到晶体学里倒格矢的表达式是怎么来的。这个解还敷陈我们矩阵值是怎么较量的，就是把行或列当成矢量求外积的究竟。对于矩阵  ，矩阵值 det(M)=(a₁i+b₁j)(a₂i+b₂j) 。此部门内容，能够扩展到随意多个变量的线性方程组，以及随意的 n×n 矩阵。

前述这些关于初等数学的处理让我感觉够神奇了，似乎我学的教科书里没有这些内容。1990年读多粒子系统理论，正式碰到数 ξ ， 有性质 ξξ=0 ，感觉可难懂得了。该数被称为Grassmann数 (的生成元)，据说是0的非零平方根。这些迷惑一向盘踞在我的心头。到了1994、1995年，闲来无事，我又读到一本New foundations for classical mechanics, 见到乘法  ，即由内积和外积两部门组成，由此喜欢上了代数几许相关的数学，才对数学物理有了进一步的懂得，并有了写一本physics for mathematics的念头。在这个过程中，我熟悉到了一位伟大的数学家、说话学家和他的学问，消解了此前心中的诸多疑问。这小我就是数学史上凭一己之力开创一个数学系统的德国中学先生格拉斯曼。前述柯西的解线性方程组的方式，以及线的代数问题以及解矩阵本征值问题的方式，都来自格拉斯曼的学问，下文会具体介绍。

格拉斯曼 (Hermann Günther Grassmann，1809-1877) 是个德国多面型学者，有名的数学家、说话学家，对物理有深刻影响 (电动力学)，职业上他是一位出书人 (图2)。格拉斯曼1809年出生于离柏林不远的Stettin小镇 (今属波兰)，几乎毕生生活在那边，其父为中学的数学、物理先生，但他显然是具有开创能力的学问家。格拉斯曼小时候跟妈妈学音乐，弹钢琴，但记忆力差也不用心。他爸认为这个十二个孩子中的老三没啥天分。格拉斯曼自1827年起在柏林大学进修古典说话、哲学与文学三年。受汗青学家August Neander和Friedrich Schleiermacher的影响，大学时代格拉斯曼对数学发生了乐趣，但没有迹象表明他曾选修过数学或许物理的课程, 却是读过一些包罗他父亲撰写的数学书和物理书。格拉斯曼1830年卒业后才算卖力起头进修数学，同时攻读数学、物理、博物学、神学和说话学，以便取得这方面的中学教师资格。1834年格拉斯曼曾接管柏林技校由数学家Jaco Steine留下的位置，因为后者到柏林大学任职去了。一说1834年起头格拉斯曼在柏林的奥托中学教数学，1847年获得高级教师 (Oberlehrer) 的称号，1852年在43岁上才在Stettin中学接替了其父的位置，获得了Professor 称号 (Professor来主动词profess, 在法语、德语里professor也用于中学先生。切实译法是讲述者、授课者)。格拉斯曼没有在大学获得教职的履历，1847年他曾写信给普鲁士教育部想弄个大学教职，但没成功。然而，格拉斯曼只手创立了一个新的数学系统 (外代数)，其意义可和缔造非欧几许与布尔代数比拟拟。他的经典著作，《扩展的学问》1844版和《扩展的学问》1862版，一向未为同时代的数学家所承认，但今天倒是诸多数学分支和数学物理的根蒂。初读格拉斯曼，你会猜忌你曾学过欧几里得几许和线性代数。问题的实情是，我学过甚至教过，然则的确跟没学过一般！此外，他照样个成功的说话学家，对照说话学学者，东方学学者，格拉斯曼翻译的《梨俱吠陀》(Rig Veda) 及长篇谈论，据大英百科全书，至今仍被研究使用。

图2. 德国数学中学先生格拉斯曼

从毕达哥拉斯到十九世纪中叶，几许学的根基问题都是若何将数付与几许，这对域论和线性代数的创立至关主要。实数的概念由荷兰人史蒂文 (Simon Stevin, 1548-1620) 于1600年完成，实数纳入几许则始于笛卡尔和费马于1630年月的工作。给几许对象付与数值非常拙笨，为此选择的原点与坐标轴不是问题自己必需的。1679年，莱布尼兹说起了竖立普适代数 (universal algebra) 的或者性，能够directly and simply 处理几许对象。莱布尼兹设想的普适代数，是想发现用较量研究图形性质的方式 (系统) ，进展能用于处理力学。

格拉斯曼的父亲老格拉斯曼 (Justus Günther Grassmann)，一位中学数学先生，也是个几许人人，可说是空间的理论 (Raumlehre) 开创者。老格拉斯曼的几许积 (geometric product) 的概念同复数的几许透露传统或许“力的平行四边形”传统之间有关联。老格拉斯曼注重到意大利数学家韦达 (François Viète, 1540-1603) 的新代数强调 “le rectangle est réellement le vrai produit de deux longueurs  (直角形(矩形)素质上是两个长度真正的积) 。” 笔者感觉可不嘛，你看那乘号× ，就是直角啊。在代数方程中，我们就是把 xx=x² 称为“x squared”的。平行四边形同正方形没有素质的分歧，它也应该是线段的某种积的究竟，而正方形只是特例。当然了，共线是另一个极限的景遇。这引出了外积的概念。老格拉斯曼的学问和著作，为格拉斯曼供应了思惟发蒙。

据格拉斯曼本身的信件，他在1832年即考虑两条或许多条线的几许和 (差) 与几许积的问题。格拉斯曼让他的一起头没有内容的形式取各类值：数，点，矢量，有取向的面、体，等等。他甚至提出了16种分歧的乘法 (保持)。格拉斯曼发现他的学问缘起于几许，然则几许只是特别应用。他的学问是以纯粹抽象的体式获得了和几许相似的纪律。打破了三维空间的限制是其长处之一。1839年格拉斯曼把这个学问弄成了能够应用到所有力学问题的水平。为了证实本身的实力，格拉斯曼于昔时撰写了Theorie der Ebbe und Flut (潮汐的理论) 一书。此书格拉斯曼固然多次提到，然则迟至1911年才得以出书。1840年，格拉斯曼写过一篇论说若何用他自1832年就起头琢磨的矢量方式来表述拉普拉斯的天体力学和拉格朗日的剖析力学这两部经典。因为发现了新的应用与扩展，加上同时忙于很多事务，格拉斯曼于1842年才起头撰写著作阐述本身的扩展的学问，1844年出书。莱布尼兹当初盼望的纳入实数的几许，由格拉斯曼几乎凭一己之力缔造出来了。1861年格拉斯曼从新从正义化的角度界说了加法与乘法，以及这些运算的连系律、交流律、分派律，这比Giuseppe Peano (1858-1932) 和 Georg Cantor (1845-1918) 早了二十多年。有一种说法Möbius, Bellavitis, Hamilton, Grassmann, Saint-Venant和Cauchy 等人都几乎自力地考虑过相似的思惟。研究念头来自几许，但亮点首要是代数的。格拉斯曼关于点的学问、点的剖析也被莫比乌斯 (August Ferdinand Möbius, 1790-1868) 自力发现，并被用分歧的体式所成长和表达过。

或许引用格拉斯曼本身的表述是得当的。“第一个激动来自对几许中的负数(量)的考虑。我已习惯了把距离AB和BA看作是相反的量。AB+BC=AC ，当A，B，C不在一条线也依然成立。当我商量几许积的这个概念的时候，这个概念已经由家父竖立 (见于Raumlehre, part I, p.174 (一说是part II, p.194)， Trigonometrie, p.10)，结论是不光是正方形，而是平行四边形，也能够看作相邻双方的积；假设边可看作是有偏向的量。迁移的概念导致几许指数量 (geometrical exponential magnitudes)， 以及导致三角函数的剖析。”

格拉斯曼把他的学问称为《扩展的学问》，笔者甚为叹服。数学，还有物理的成长一向在示意扩展的过程。这个扩展，是空间的扩展，对象的扩展，系统的扩展。仅仅从直线段上的 AB+BC=AC ，他就想到不共线时也应该成立，就是一种扩展。若 x+y=c 里都是数或许量 (numbers or magnitude)，这就是关于数或许量的代数。在 (A-B)+B=A 中， A透露点，  (A-B) 透露矢量，这就是透露几许的代数。这也是一种扩展。克利福德后来将加法扩展到分歧阶 (grades) 的量上，引入了新的几许积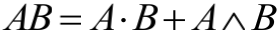，也是一种扩展，首先是对格拉斯曼工作的直接扩展。由线段的简洁关系AB=-BA^（3），后来就扩展到关于格拉斯曼数，这可用于描述费米子，还被用于扩展而得超空间、超对称性的概念。用扩展的目光看数学与物理，会有面前的景致一时通亮了起来的感受。

5.1 线之积

我们如今商议线之积 (linear production)。面、体乃线之积，却弗成所以点的积。就线之积而言，显然 ξξ=0 ，一条线和它自己组成的面之面积为0！格拉斯曼初始考虑线之积的时候，发现乘积的交流律有 e_ie_j=e_je_i 和 e_ie_j=-e_je_i 两种或者的选择。考虑到 P(e_ie_j)=e_je_i ；PP(e_ie_j)=e_ie_j  ，故 p²=I 是个全等把持，是以有 e_ie_j=e_je_i 或许 e_ie_j=-e_je_i 这两种选择。有了看似反常的 e_ie_j=-e_je_i，我们早年习认为常的 e_ie_j=e_je_i 才浮现其真义，这如同有了广义相对论，早年的相对论才作为狭义相对论获得了更好的懂得。注重，格拉斯曼的选择 e_ie_j=-e_je_i 包管 e_ie_i=0 ，这相符对线之积的要求。顺着这个设法，就能够懂得在三维景遇，若存在三个基 e₁, e₂, e₃，则算法 e_ie_j=-e_je_i 使得只存在一个自力的三阶单元 e₁e₂e₃ ，且它强制 e₁e₂，e₂e₃ ，e₁e₃ 是线性自力的，因为若 ξ₁e₁e₂+ξ₂e₂e₃ +ξ₃e₃e₁ =0，离别乘上  e₁, e₂, e₃ 中的一个就能证实个中的系数都必需是0。我上大学学线性代数 (对格拉斯曼代数的选择性成长) 时，书中曾说起线性不相关，却没有敷陈我们怎么证实。参照上面证实可知，若线元素a₁, a₂, …,a_n 是不相关的，当且仅当 a₁, a₂ …a_n≠0。

顺便提一句，英国数学家怀特海 (Alfred North Whitehead，1861-1947) 排斥 e₁+e₁e₂ 如许的具有分歧阶的形式 (forms of mixed degree)，然则克利福德接管如许的和的形式, 遂有了更壮大的代数。这一套思惟被David Hestenes (1933-) 用于经典力学，算是终于圆了莱布尼兹的妄想。我们一样所说的线性空间，线元素的分歧阶的积被划归分歧的graded linear space (单阶的线性空间)。好比，对于三个基 e₁, e₂, e₃ 的景遇， e₁, e₂, e₃组成一个三维空间；e₁e₂ ，e₂e₃ ，e₁e₃ 组成一个三维空间，而 e₁e₂e₃ 组成一个一维空间。

5.2 外积与内积  

格拉斯曼引入了外积的概念。先是点的外积。AB=A-B 是从点B到点A的一个矢量 (not a vector from A to B, but as a vector limited to positions in the line through A and B, that’s line-bound vector! 矢量, vector, 是哈密顿为了他的四元数在同时期引进的一个词儿)，然则因为有AA=0 ，AB=-BA ，显然这个 AB=A-B 就是外积。接着是矢量的外积。对于随意多个矢量，外积为0意味着它们必是相关的。格拉斯曼指出，外积的特征是有如下性质：两个相关的量，其外积为0。当然了这个性质不是积的必然性质，还能够界说其余积。

格拉斯曼1844年的外积比他1840年的几许积更抽象、更普遍，后者只是一个特例。他还考虑了外除 (outer division)，由此通俗的数进入了他的系统。如今的几许积是克利福德意义下的， ，即几许积为内积与外积之和。顺便说一句，外积  描述的是a, b之间的connection (这个词在微分几许那边所指的概念，汉译联络)。格拉斯曼展示了若何用外积来解n个变量的线性方程组 (见第二节里柯西的解法)。商议外积还要说起分派律 e_x(e_y+e_z)=e_xe_y+e_xe_z 和连系律 e_x(e_ye_z)=(e_xe_y)e_z。

格拉斯曼用两种体式引入内积。其一是借助投影。两个矢量组成小面，在夹角改变时视察一个矢量在另一个矢量上投影的转变；其二是求补 (complementary)，考虑的是空间的完整性。对于一组基 e₁, e₂, …,e_n，知足外积的性质，则界说合成元素 E 与其补 |E 老是知足关系 E|E=e₁e₂…e_n 。因为这就是个1维的线性空间，故可被看成一个标量，而 e₁e₂…e_n 能够无需显式地写出来。所以，若是有两个元素都是具有沟通阶的形式 (forms of the same order)，则总有 E|F=α 为一标量。显然有 。对于一阶的形式，即矢量，有 ，这就是我们熟悉的、后来线性代数里的矢量内积，是一个特例。在现代说话里，格拉斯曼引入的这个求补把持，称为Hodge star operator。

格拉斯曼是第一个揭橥了点乘 (标量积) 的人。他将之称为内积，因为只有当两个偏向互相接近时，这个积才不为0。我猜，格拉斯曼是注重到，当一个线段从另一个共点的线段上出发，扫过一个角度去张开一个平行四边形时，它在另一个线段上的投影也一向在变——从出发处的整个长度变互相垂直时的为0。这个投影与投影在其上的线段之积是一种新的积，因为它交流脚色后符号不变。

能够从共点的两线段从重应时将其一逐渐打开张成一个平行四边形的过程来看外积和内积。外积对应所张的有取向的平行四边形的面积，为交流否决称的，过程起头时对应的外积为0。然而面积并不克完全确定这个平行四边形。内积为两线段之一与另一者在其上投影的乘积，过程起头时应取极大值，为交流对称的。内积为0是两线段 (矢量) 垂直的判据；外积为0是两线段 (矢量) 平行的判据。

5.3 关于矩阵本征值问题

考虑空间从一套基到另一套基的变换，格拉斯曼就把它写成  的形式，能够获得它的矩阵透露。接着他就注重到了求解矩阵的本征值和本征矢量的问题。对于一组基 e₁, e₂, …,e_n 下的本征值问题  ，个中  是个矢量。记 ，本征值问题  对应关系 ，这解说 c₁, c₂, …,c_n 是相关的。按照格拉斯曼的理论，其外积为零，，然则 e₁e₂…e_n≠0，那天然是系数为零，也就是 。分歧本征值对应的本征矢量是自力的，是以一个算符 (矩阵) 的空间能够分化为不变子空间的直和，而一个不变子空间对应沟通的 (简并) 本征值。由此能够证实对称矩阵的谱定理 (spectral theorem)。该定来由Weierstrass 1858年证实，n个分歧根的景遇是由柯西于1829年证实的，格拉斯曼证实的 primary decomposition theorem 以及 Jordan的正则形式 (canonical form) 都揭橥于1870年。这一切为原子谱学和量子力学预备好了数学根蒂。矩阵力学、希尔伯特空间，不外是这些工作的天然延伸，属于摘现成的桃子。那些量子力学的缔造者，不外是经典力学和经典数学刚巧都几多学了一些罢了。

格拉斯曼组织的是一个全新的数学系统。他发现那不是几许，而是一门新的科学，几许只是一个应用范畴罢了。格拉斯曼测验过多种分歧的示意形式，最终于1844年出书了《扩展的学问》 (图3)。无疑地这是一本经典(请记住作者是说话学家)，然则格拉斯曼要做的是成长一个广大的新系统，并且思惟还欠好提掏出来 (新思惟的表达需要新概念、新说话系统以及新的表达体式)，为此该书起头还有哲学的铺垫，故而这本书固然思惟内容雄厚，但可读性值得商榷。这本书其时印了几多册已无可考，但显然鲜有人问津。1844版的出书人在1876年给格拉斯曼的信写道：“您的著作Ausdehnungslehre无存货已有一段时间了。因为您的鸿文几乎无人问津，大约有600本在1864年被当成废纸用了，剩下的那么几本比来卖出去了，我们的书库里还有一本。”

格拉斯曼本人一向在测验为本身的学问找到得当的表述体式，其《扩展的学问》1862不是1844年版的重印，而是重写。令人可惜的是删掉了此前的哲学阐述。所谓的《扩展的学问》1862，应该在1861年就有了，在那年10月格拉斯曼就送了一本给莫比乌斯，不外有300本上印着的日期是1862. 《扩展的学问》1862全名为Ausdehnungslehre：vollständig und in strenger Form bearbeitet (扩展的学问—以完整、严谨的形式呈现的)，不外迎来的照样失望，甚至比第一本书更少受到存眷。《扩展的学问》1844的第二版于1878年注销，那时格拉斯曼已经作古了。《扩展的学问》1844和《扩展的学问》1862可作为两本书对待。

用后世的目光来看，格拉斯曼是几许较量、外代数、矢量空间理论的奠定人。作为一个知道本身做出了伟大成就的中学先生，他想获适合世数学家承认的表情估量是强烈的。然而，如同阿贝尔，伽罗华，康托一般，格拉斯曼是那种十九世纪不幸的伟大数学家，直到其辞世的1877年，格拉斯曼的数学所获得的承认几乎是聊胜于无。有一种说法是，格拉斯曼遭遇的是非同平常的轻忽 (colossal neglect)。

格拉斯曼的《扩展的学问》1844几乎没受到什么存眷。他一定是送了一本给高斯的，高斯在1844年12月14日回答道：“我曾在半个世纪前考虑过相关问题，并于1831年就揭橥过一些究竟。”高斯指的或者是他在复数的几许透露方面的工作。大数学家莫比乌斯应该是对格拉斯曼很早就有所耳闻，1839年，他评价钱拉斯曼的晶体学工作很有意思。当然，晶体学首先就是关于空间堆垛的问题，而空间学是格拉斯曼父子考虑的主题。格拉斯曼1644年送了莫比乌斯他的《扩展的学问》，莫比乌斯也是作了谈论的：“对于格拉斯曼著作中作为数学元素根蒂的哲学元素我无意用准确的体式予以赞赏，甚至不克准确懂得。”莫比乌斯认为格拉斯曼的著作贫乏直观性 (intuition, Anschaulichkeit) 这个数学思惟的根基特征, 他不得不跳过那些格拉斯曼称为extension或许generality的器材。其实，愚认为，extension and generality (扩展与一样性)，这后来都成了数学的传统了, 什么器材都有个generalized 版本，连相对论都未能逃脱这个命运。这恰是格拉斯曼伟大的处所啊。有能力处理一样性和抽象，才是大科学家！

1846年，莫比乌斯邀请格拉斯曼列入一场数学角逐，解决一个由莱布尼兹提出的问题：发现一种不消坐标和度规性质的几许算符 (莱布尼兹称为analysis situs, 便是后来的拓扑学) 。这个思惟，不恰是后来广义相对论要呈现的思惟嘛！格拉斯曼以一篇Geometrische Analyse geknüpft an die von Leibniz erfundene geometrische Charakteristik (同莱布尼兹所发现的几许特征相关联的几许剖析)胜出，但被莫比乌斯指摘其使用了抽象符号而未对读者交卸为什么这些符号是有价格的。格拉斯曼固然凭这篇胜出 (似乎是为他量身定做的，只有他一份谜底)，但没对他的命运带来改变。

就几许代数而言，有三小我是必需提到的，格拉斯曼、爱尔兰的哈密顿与英国的克利福德。哈密顿在1843年发现了四元数。格拉斯曼思虑空间的学问，把几许看成代数；哈密顿考虑时间，把时间作为纯粹的代数 (pure algebra)，不知时空的概念是不是也能发生什么新颖的代数。哈密顿获得一本《扩展的学问》1844版，感觉欠好懂，他曾写信给August de Morgan (1806-1871)，说为了能读格拉斯曼他或者不得不学抽烟。1852年哈密顿读格拉斯曼的书，一些谈论揭橥在他的Lectures on quaternions (1853) 的前言中了。哈密顿认为这是能够和他的与四元数相关的工作相提并论的成就，如今是读起来with admiration and interest. 这应该算是对格拉斯曼学问的承认，或者是因为谁人时代交流未便，这个1835年30岁上就册封的爱尔兰数理大神的承认没能对格拉斯曼及其学问的命运发生实时的影响。

格拉斯曼的《扩展的学问》是他生命的倾情贡献。到了1861年，格拉斯曼对他的成就所遭到的冷遇是有点怫郁的。格拉斯曼在他的《扩展的学问》1862版前言中写道 (大意) ：“我坚信就算再过17年甚至更长的时间这本书无人问津，不克进入科学的正轨，有一天它也会从遗忘的尘埃中被发现，现在沉睡的思惟终会开花究竟。……因为真理是永恒的、神圣的(Denn die Wahrheit ist ewig, ist göttlich......)，真理的任何发育阶段都不会不留陈迹。”

在盛产数学家的德国及周边区域，格拉斯曼所创立的学问要说无人识货，这也不正常。其实，1860年意大利的Cremona, Bellavitis 和 Peano等人对格拉斯曼的著作就发生了乐趣。1866年德国青年汉克尔 (Hermann Hankel, 1839-1873) 来信赞扬格拉斯曼的阐述，并要求其能进一步整顿，这算是对格拉斯曼的认可，但那时汉克尔不敷分量。1869年，克莱因 (Felix Klein, 1849-1925) 注重到了汉克尔Vorlesungen über die complexen Zahlen und ihre Functionen (复数与复函数教程) 一书中提到了格拉斯曼的名字。克莱因向克莱布什 (Alfred Clebsch, 1833-1872) 介绍了格拉斯曼，还跟Sophus Lie说起格拉斯曼的工作。后来，克莱因坦诚深受格拉斯曼的影响，甚至影响了他1872年的埃尔朗恩纲要。1871年，经由克莱布什介绍，格拉斯曼入选了哥廷恩科学院的通信成员。至此，格拉斯曼算是获得了承认，不外格拉斯曼在1877年就过世了。1878年克利福德出书了“格拉斯曼睁开代数的应用” (une Application de l'algèbre de l'extension de Grassmann ？？)，美国留学生吉布斯和克莱因一路在1894-1911年间整顿了格拉斯曼的著作。到了1870年月中期，在英国也有Hermann Noth (1840-1882)、William Kindgdon Clifford (1845-1879)、W. Preyer (1841-1897)等人对格拉斯曼的工作发生乐趣。注重这些数学家大多在50岁前就作古了。这些数学家，如同北极冰雪下的植物，在极短的生命里早早地开出极为光耀的花朵，结出能够保持下一个春天的果实！

1878年，格拉斯曼的《扩展的学问》1844版的第二版出书。格拉斯曼在前言中提到黎曼的学生汉克尔在1867年论说复数系统的理论 (Theorie der complexen zahlensysteme) 时强调了其学说的主要意义，1/10的内容用于介绍格拉斯曼的工作。这解说，格拉斯曼临终岁月里是知道本身的著作已经被人接管了的，这些几多对格拉斯曼是个抚慰。

格拉斯曼之成就与著作的未被承认，反映在其人的际遇上。固然几经测验，但终其平生，格拉斯曼都未能在大学谋到一个教数学的差事。发现格拉斯曼价格的汉克尔和克莱布什不久年数轻轻就辞世了；德国的莫比乌斯、英国的哈密顿和意大利的Bellavitis 够分量，但在别处有要首倡和拥护的器材；而热心肠的Victor Schlegel (1843-1905) 人微言轻，热情跨越能力。其实，这种革命性的发现被轻忽，汗青上早有先例，这也不是破例。然而，正如格拉斯曼所坚信的那样，真理是永恒的。今天的数学物理范畴，格拉斯曼所创立的数学是个中光耀的瑰宝，格拉斯曼的学问会为有心数学与物理的人们供应源源不尽的灵感。

研究格拉斯曼让我对线性代数这个全世界理工科人都要进修的科目有了新的熟悉。2020年12月19日我熟悉到所谓的线性代数是对lineale Algebra (linear algebra) 的错误翻译，准确的翻译是“线之代数”，即人家本意的algebra about line segment，一时间怅然若失。这个学问来自数与点、数与线乘积的扩展。就着错误的概念进修，不领略一门学问的缘起，延迟了几多人的贵重时光。想起了那句《西纪行》的名言，“不闻至人传妙诀，空教口困舌头干！” 学问是讲究传承的，这一点不服不成。

我们小时候学过一点浅浅的几许与代数，浅得连根基的经典力学入门都不敷用，殊不知几许、代数本是一体的。不克剖析几许的代数不是真正的代数，and vice versa。格拉斯曼、哈密顿和克利福德奠立的几许代数，是能用于几许的代数学；与此相对，代数几许 (algebraic geometry) 则行使抽象代数手艺研究多变量多项式的零点鸠合的几许问题。你眼里是看到代数照样几许，是几许代数照样代数几许，照样个浑然一体，全在于你本身。格拉斯曼的代数更适于物理，因为它区分矢量与赝矢量。对矢量和赝矢量不加区分，让电磁学理论始终是一团糊涂酱。用矢量导数及逆矢量导数透露的麦克斯韦方程组不妨认识一下。

线之代数是用于几许的学问，如仿射几许、欧式几许，然则现在的一些版本里面矢量是主要的，而点竟然是无关紧要的了。线之代数是线段&实数的学问。线之代数用于函数空间，例如希尔伯特空间，那边就没有点的事儿，作为复值函数的波函数叠加  是竖立在复数域上的，这个与线段 (矢量) 一同显现的数是若何从实数扩展到复数域的，我似乎未见哪本量子力学书有过商议。

我注重到一个事实，1834年在奥托中学时，格拉斯曼同时教数学、物理、神学、德语和拉丁语。写到这里，我稀奇想借此机会说出我的概念：“我们的社会该提高对教师的要求了。”多专多能的先生才是及格的。若是我们甘愿贯彻这个理念，我们的国度将是以受益无限，而首先受益的将会是我们的中小学先生们本身。

格拉斯曼博学、高产。除了重点介绍的《扩展的学问》和《梨俱吠陀》译本，1844-1861年间格拉斯曼揭橥了17篇包罗物理学的科学文章，还有一些数学和说话的教材，包罗1861年的Lehrbuch der Arithmetik (算术教程)。哦，为了评价钱拉斯曼的高产，有需要顺带提一句：格拉斯曼于1849年娶亲，除了发生了那么多的思惟成就以外，还连生了11个孩子。这一点，他也是继续了其父的长处，他是12个孩子中的老三。格拉斯曼继续了父亲的数学思惟，成为一个数学范畴的开创者，但一生未能谋到一个大学教职；后来他的一个儿子 (Hermann Ernst Grassmann) 成了数学传授，算是圆了他的妄想。

注：本文改写自曹则贤著《磅礴为一》一书。

[1] Michael J. Crowe, A history of vector analysis, Dover Publications, Inc. (1967).

[2] Vincent Pavan, Exterior Algebras: Elementary tribute to Grassmann’s ideas, ISTE (2017).

[3] Alfred North Whitehead, A treatise on universal algebra with applications, Cambridge (1898).

[4] Hermann Günther Grassmann, Gesammelte mathematische und physikalische Werke (数学物理全集), 3 Bde., Friedrich Engel (ed.), Teubner (1894–1911).

[5] Hermann Günther Grassmann, Geometrische Analyse geknüpft an die von Leibniz erfundene geometrische Charakteristik, (1847).

[6] Hermann Günther Grassmann, Die lineale Ausdehnungslehre, ein neuer Zweig der Mathematik, Wiegand (1844). English translation by Lloyd Kannenberg, The linear extension theory: A new branch of mathematics, Open Court (1995).

[7] Hermann Günther Grassmann, Die Ausdehnungslehre. Vollständig und in strenger Form begründet, Enslin (1862). English translation by Lloyd Kannenberg, Extension Theory, American Mathematical Society (2000).

[8] Hans-Joachim Petsche, Gottfried Keßler, Lloyd Kannenberg, Jolanta Liskowacka (eds.), Hermann Graßmann Roots and Traces: Autographs and Unknown Documents, Birkhäuser (2009).

[9] August Ferdinand Möbius, Der barycentrische Calcul, Leipzig (1827).A. Fraenkel, Über die Teiler der Null und die Zerlegung von Ringen, J. Reine Angew. Math., 145, 139-176(1915).

[10] Henry George Forder, The calculus of extension, Cambridge (1941).

[11] Otto F. Fischer, Universal Mechanics and Hamilton's Quaternions, A Cavalcade (Stockholm, 1951).

[12] Otto F. Fischer, Five Mathematical Structural Models in Natural Philosophy with Technical Physical Quaternions (Stockholm, 1957).